此文档创建于 2022/8/17

编程语言的设计和实现

语法和语义

我们在讨论什么:

语法 (Syntax)
语义 (Semantics)

什么是语法 (Syntax)

语法 (syntax) 是指代码文本的规范，只有符合语法的代码才可能被编译器/解释器处理。

例如，a = 1; 是C语言的赋值语法，而 a := 1 在C语言中不合法。

其中，一个重要的概念是语法结构，它通常以语法树 (syntax tree) 的形式展现:

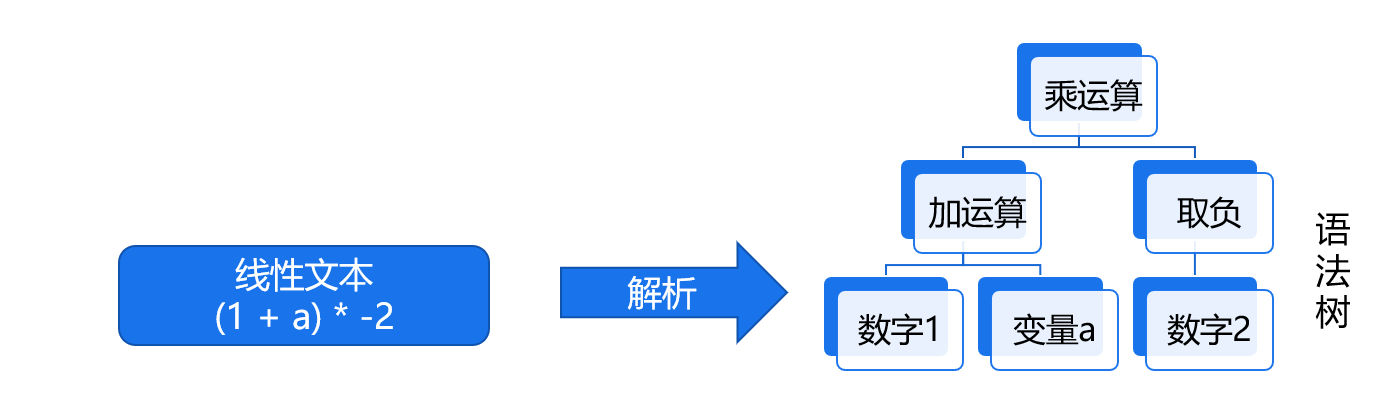
AST Tree

语法和 BNF

语法规则通常使用 BNF 文法定义。下面是四则运算的 BNF 文法：

e : addsub

addsub : addsub '+' muldiv
       | addsub '-' muldiv
       | muldiv

muldiv : muldiv '*' atom
       | muldiv '/' atom
       | atom

atom : '(' e ')' | NUMBER

以下是此知识点涉及的习题，带着习题学习，能方便自行评估学习的效果。

习题

"(1 + 1) + 1"是否是合法的四则运算语言文本？
"(1 / 2) + 1"是否是合法的四则运算语言文本？
"1.2"是否是合法的四则运算语言文本？
如果"1 + 1.2"对应语法树是 Add(Int(1), Float(1.2))，

问："1 + 1.2 * 2"的语法树是？

抽象语法树和具体语法树

根据BNF文法，我们将语言的文本解析为语法树——文本在语法规则下的结构化表示。

常用的语法树有两种：

具体语法树 (CST)：除开结构化语法外，事无巨细地记录源代码信息。CST可以无损地转回源代码。
抽象语法树：只考虑后续工作需要的语法结构，抛弃了 CST 中对下游任务冗余的信息，如空白符，分隔符，缩进等。

举例子，给定一个语句 a = 1;, CST 与 AST 的差异通常如下图所示。

具体语法树	抽象语法树
`Statement( kind = "assign", children = [ Variable("a"), Token("="), IntLiteral(1), Token(";") ] )`	`Assignment( target=Variable("a"), value=IntLiteral(1) )`

为了方便理解，上述两种语法树均进行了简化（例如略去行列号等），但仍然不难看出，抽象语法树的信息比具体语法树更少，也更加紧凑。

在涉及语法树的主要任务是编译、解释与各式代码分析，此类应用属于主流，一般只会用到抽象语法树，而无需具体语法树¹。这意味着语言的具体语法通常不影响语言的运行。

一门编程语言可以拥有多种具体语法，只要他们的语法结构和语义相同。语法不同、而语法结构与语义相同的语言之间，差异是表面的、不重要的，例如 f(x, y, z) 和 call f with x, y, z。

什么是语义

Tip

语义是对语法结构的解释。
解释方式是多样的，不同的语义产生不同的解释。

解释方式是多样的，例如，打印语法树是一种可行的解释。

但在通用编程的语境下，人们一般关注的解释方式是代码执行 (evaluation) 。

不管对语法结构做何种解释，需要一套规则来描述解释过程。

以下框架提供了描述语义的常见手段:

语法结构 $X$ 的执行结果是 $r$ $\Longleftrightarrow$ $X \rightsquigarrow r$ .

这里的 $X$ 是一个语法结构，如果对应编程概念，它是 host language (实现编译器、解释器所使用的语言) 中的一棵语法树 ²。

$X \in \text{语法树全集}$

这里的 $r$ 是一个值，如果对应编程概念，它是 target language (编译器、解释器运行最终代码所使用的语言) 中的一块运行时数据。为了方便，接下来的讨论中，我们会预设 target language 是 Python ，以方便读者理解在 $r$ 上做的各种变换。

$r \in \text{Target Language值全集}$

上面这个框架，表达四则运算语言的语义绰绰有余：

$\text{Add(Number(2), Number(2.0))} \rightsquigarrow 4.0$

但是，由于语法结构的具体数目是无限的，我们不能一一列举所有的语义规则。因此，我们需要采取一种递归的方式来描述语义，让这套递归规则能够覆盖所有的语法结构。

下面，我们依然以四则运算语言为例，给出一套可行的递归规则，介绍相继式 (sequent) 和操作语义 (operational semantics)。

相继式和操作语义

对于大多数语言来说，合法的语法结构是无限的，想想也知道，我们不能在一个语言规范手册里写下：

$\text{Add}(1, \text{Add}(1, \text{Add}(\cdots, \text{Add}(\text{Number}(1), \text{Number}(1))))) \rightsquigarrow 2992$

这里我们需要一个“注意到”。

Tip

注意到语法结构的定义是递归的。因此可以定义出一套递归的、有限的规则，为合法语法结构的全体描述语义。

为了做到这一点，我们介绍相继式：

$P_1, P_2, \cdots, P_n \vdash Q$

这里的 $P_1, P_2, \cdots, P_n$ 是条件 (前件)， $Q$ 是结论 (后继)。

上面的公式，在逻辑上是一种断言 (assertion)，它表明在条件 $P_1, P_2, \cdots, P_n$ 都成立的情况下，基于规则 $\vdash$ 的推导能得到 $Q$ 。

相继式更重要的用途是描述推导过程，在实践上，你可以使用前件和后继这样的术语来强调 “现在我在讨论规则推导”。

形如 $P \vdash Q$ 的相继式，其整体可以作为条件，服务于更复杂的推导。例如，假设 $c_i$ 是一个相继式，那么我们可以有如下的推导：

$\dfrac{c_1 \;\; c_2 \;\; c_3 } {c_4} \Longleftrightarrow$ 在条件 $c_1 c_2 c_3$ 都成立的情况下，推导 $c_4$ 成立。

基于相继式，推演的逻辑可以层层嵌套，方便我们用一种规范性的方式，来描述包括编程语言语义在内的任何逻辑规则。

四则运算的操作语义

在开始之前，我们需要定义一些元符号 (可以大致理解为宿主语言中的变量)，来让规则变得容易被纸笔描述：

\begin{aligned} & i, i_1, i_2 \cdots i_n \in \text{实数} & \\ & X, Y \in \text{四则运算语言的语法结构全集} & \\ & f(i_1, i_2),\; f \in \{\textbf{+, -, *, /}\}\;\; \text{表示实数的加/减/乘/除} & \\ \end{aligned}

借助这些元符号，我们定义四则运算语言的完整语义(乘法，除法，减法被省略)：

\dfrac{X \rightsquigarrow i_1 \;\; Y \rightsquigarrow i_2 }{\text{Add}(X, Y) \rightsquigarrow \textbf{+}(i_1, i_2) } \qquad \dfrac{ }{ \text{Number}(i) \rightsquigarrow i}

此处有一些简化，不看也不影响:

$\rightsquigarrow$ 两侧出现的 $i$ 实际上是不同的。他们身处不同的语言，就像文本 1 与 C++ 运行时整数 1 截然不同。在论文中， $\rightsquigarrow$ 左侧的 $i$ 常常表示一个文本，而右侧的 $i$ 表示一个 target language 中的数字，论文常常是有点过度严谨的，因为不仅需要从头定义 target language 的数据结构，还需要在推断过程中体现字面量的求值过程。

带状态的语义

在 Java 和 C++ 语言中，我们可以修改对象的字段。这是一种副作用，副作用会引起某些函数在参数相同时、返回值却不同。

static struct MyTypeRef *val = { ... };

int some_func(int factor)
{
    return val -> a * factor;
}

int main()
{
    int result1, result2;
    result1 = some_func(2.0);
    val -> a = 1; // 对象val的字段a被修改
    result2 = some_func(2.0);
    // result1 != result2, 副作用！
    return 0;
}

可以看到，C++ 的语义是有副作用的，因此我们方才介绍的 $X \rightsquigarrow r$ 这套表述不足以描述 C++ 语义：我们原先只考虑了返回值，但一些语言中，语义涉及到副作用。

副作用的本质是函数调用被隐式地增加了如下部分：

一个参数: 表示全局状态
一个额外的返回值: 表示函数修改后的全局状态

因此，当我们在 C++/JavaScript/Python 等主流语言中写下 f(arg) 的时候，我们实际上写下了类似 [GLOBAL_STATE, result] = f(GLOBAL_STATE, arg) 的代码。

对于具有副作用的语言，程序行为受全局状态影响。按照 PL 领域惯例，语义描述通常要求规则是完全透明的，没有隐式的预设，因而语义应当能够完全决定程序行为。所以，带有副作用的编程语言，在描述语义时必须同时描述全局状态的转移。在这种情况下，描述语义的框架通常是：

(S, X) \longrightarrow (r, S)

该框架是非常痛苦的，因为如下四点：

需要考虑的变量变多
需要使用的符号变多
推导公式将变得冗长
描述副作用很无聊

上述第4点中的“无聊”一词并非情绪表达，而是一种通用的见解：TLDR; 副作用不是关键。

副作用在直观上理解起来非常容易，关于这一点，当下编程语言的流行情况已有明证；但是，要想使用公式系统将副作用描述清楚，工作量将会倍数增长，但关键的信息，如推导流程、情况分类、特殊语言特性等，却大同小异。

因此，在此段落后，表述将追求关键而不求精准。这就是说，虽然我们仍使用 $(S, X) \longrightarrow (r, S)$ 来描述关键状态的变化，但对于一些特殊的、我们不关心的副作用，例如 IO 等将被有意忽略。例如，当我们处理打印语句时，这里应当出现了一个函数调用，此调用实际做了打印、引发了副作用，但我们不关心这一点并将其视为一个空返回值的纯函数。

所幸的是，这种“不正确”丝毫不影响我们精准地理解程序语言的语义，它是一种折衷。

如果你真的需要“更正确”的框架描述来描述具有副作用的语言的语义，你可能需要接触Haskell的副作用观点，它巧妙地将副作用表示为状态初值

S_0

上发生的一系列变换：

S_n = \textit{eff}_n(\cdots, \textit{eff}_2(\textit{eff}_1(S_0)))

。

此外，为了方便介绍，在本文后续部分，我们将认为语法结构是 host language 中的数据结构，而状态 $S$ 及返回值 $r$ 是 target language 中的数据结构。更进一步地，我们让 host language 等于 target language，这样一来，前文中 $\text{Number}(n) \rightsquigarrow n$ 的含义就非常明确了。

LC的语法解析

欢迎来到编译器最平凡的部分，语法解析 (parsing)。

除开产出学术成果的研究需要，否则强烈建议不要在 parsing 上浪费任何的时间。

实用主义的 parsing 技术选型

解析器从源代码文本中提取语法结构，这个语法结构通常指抽象语法树。

相应的语法解析技术，具体来说有很多，例如手工递归下降法、parser generator 和 parser combinator 等。

通常来说，解析器需要着重报错与表达力，但对极限性能的需求则相当虚拟。使用ANTLR4 (一个实用的 parser 生成器框架)，按照 lua 规范实现一个 lua 解析器，这样的解析器中会存在相当多的歧义，多少会导致性能问题。但在实践中，上面这样“低质量”的 lua 解析器一秒钟能解析接近10万行来自 real world 的工业代码，这种性能足以让 IDE 分析工具在你每一次落键瞬间重新解析、分析当前文件并更新补全信息。

因此，建议读者大胆地去使用那些表现力足够强、报错足够好的解析器生成器，例如 ANTLR4, Python Lark 等等；parser combinator/parsec 也可以用，报错机制会更灵活，但做事情会慢一些；需要小心那些 LL(1)/LR(1) 解析器，如果你不算parser 专家，或者不想浪费生命去纠结为什么你的文法不工作。

此文章将使用 Python 的 Lark 来演示。它的性能其实非常差，但因为非常实用，被大量重要的 Python 开源项目使用 —— 从这里也可以看出，解析器性能很多时候并非关键。

基于 Python Lark 来解析 LC 语法

start : lc

lc    : call
      | atom

call   : call atom
       | atom

atom  : CNAME
      | func
      | prim
      | number
      | boolean
      | string
      | "(" lc ")"

string : ESCAPED_STRING
number : NUMBER
boolean: "true" | "false"
var    : CNAME
func   : "func" "(" CNAME ")" "{" lc "}"
prim   : '@' CNAME

%import common.WS               // 这是空白符token
%import common.ESCAPED_STRING   // 这是双引号字符串token
%import common.CNAME            // 这是C标志服token
%import common.NUMBER           // 这是数字token
%ignore WS                      // 忽略所有空白符

这个文法被一行代码的 Lark 编译工具处理后，可以生成一个 LC 语言的解析器，具体可参考 json_parser全流程。由于这个解析器输出的是具体语法树 (CST)，你可能需要手动转换CST到AST。

出于可读性和可维护性的考虑，CST 到 AST 的转换最好在文法中进行 (参考语法制导，或semantic actions)。虽然关于这一点常常有一些相反意见，但Python的发展生动地说明了这点。对此，我的建议是努力地使用语法制导，但绝不在文法中引入构造 AST 以外的逻辑。

// 一个好的使用semantic action的例子
lc_atom : CNAME   -> Var(token_to_string($1))
        | "true"  -> BoolVal(True)
        | "false" -> BoolVal(False)
        | ...

现在，使用 Lark 或者别的你觉得趁手的解析器生成工具，为 LC 语言生成一个解析器。

如果你觉得这个工作很无聊或者不好办，可以无情地使用以下步骤获得一个 parser：

安装 Python 并激活环境: https://conda-forge.org/miniforge
创建一个项目文件夹 intp_exercise。
新建lc_ast.py，将扩展LC语言的所有语法结构 (Call, Prim, Var, Func, NumberVal等) 以及前面 eval_lc 函数，放入 lc_ast.py 中。

在文件夹中创建文件 lc1.lark，在文件夹中创建文件 lc1.lark，内容如下:

%%
from lc_ast import *
%%

start : lc             -> $1
lc    : lc atom        -> Call($1, $2)
      | atom           -> $1
atom  : CNAME          -> Var($1.value)
      | '@' CNAME      -> Prim($2.value)
      | NUMBER         -> NumberVal(eval($1.value))
      | "true"         -> BoolVal(True)
      | "false"        -> BoolVal(False)
      | ESCAPED_STRING -> StringVal(eval($1.value))
      | "(" lc ")"     -> $2
      | "func" "(" CNAME ")" "{" lc "}" -> Func($3.value, $6)

%import common.WS               // 这是空白符token
%import common.ESCAPED_STRING   // 这是双引号字符串token
%import common.CNAME            // 这是C标志服token
%import common.NUMBER           // 这是数字token
%ignore WS                      // 忽略所有空白符

运行命令 pip install lark-action, 安装 lark-action 包

在文件夹intp_exercise/下运行：

python -m lark_action lc1.lark --package="" --module="lc"

lc_run.py 内容如下：

# lc_run.py

from lc import parser
from lc_ast import eval_lc

def add(ctx, x):
    def addx(ctx, y):
        return y, ctx
    return addx, ctx

S = { 'add': add }

def run_code(source_code):
    r, _ = eval_lc(S, parser.parse(source_code))
    print("执行结果为:", r)

run_code("add 1 2") # 3
run_code("(func (x) {add 2 x})(3)") # 5

执行命令 python lc_run.py。

按照上述步骤，你将可以运行扩展后的 LC 语言，前提是你完成了扩展 LC 的解释器实现 (Python)的代码习题。

改动 lc_run.py 的代码，多看看效果。

习题

尝试实现一个REPL (Read-Eval-Print-Loop)。

更丰富的语言构造: 变量绑定、if, while

虽然我们已经完成一个有模有样的解释器，但它目前仍很不实用。

该如何赋值呢？我们甚至不能使用 x = 1 这样的代码。

此外，函数体也只能支持“一句话”，而不能支持多行，就像下面这样：

func (x)
{
    display x
    add x x
}

要支持上述能力，我们引入两种新的语法结构：

变量绑定

语法结构: Assign(name: str, expr: LC)
语义:
$\dfrac{ S, X \longrightarrow r, S' }{ S, \text{Assign}(a, X) \longrightarrow r, (a \mapsto r) S' }$

语句块

语法结构: Block(body: list<LC>)
语义:
$\dfrac{ S_0, X_1 \longrightarrow r_1, S_1 \quad S_1, X_2 \longrightarrow r_2, S_2 \;\cdots\; S_{n-1}, X_n \longrightarrow r_n, S_n }{ S_0, \text{Block}(X_1 X_2 \cdots X_n) \longrightarrow r_n, S_n }$

习题

尝试在 lc1.lark 中为 Assign 和 Block 加入合适的语法规则，以支持下面的代码：

func (x)
{
    x = add x x;
    x = add x 1;
    x
}

习题

尝试实现以下语言扩展，让我们的语言看起来更“工业界”：

具名函数：目前实现的LC解释器，函数均为匿名
if语句
while语句
return语句
多参数函数
break, continue

此外，还可以实现相应的REPL以及文件输入执行功能。

本页面已帮助我的一名实习生掌握了基本的编译、解释技术，项目链接如下，可作为参考实现：

https://github.com/April-ZhouQian/interpret

在后续章节，我们将基于上述参考实现，实现相应语言的字节码编译器。

字节码编译 (待完成)

如果运行前面解释器的参考实现，可以发现，性能比Python还要低好几个数量级。

LC = Call(func: LC, args: LC)
   | Var(varname: str)
   | Func(argname: str, body: LC)
   | BoolVal(value: bool)
   | NumberVal(value: number)
   | StringVal(value: str)

回顾语义的描述方式，我们使用 $S, X \longrightarrow r, S'$ 的表述框架，而编译可以视为对这个过程的一个拆解。

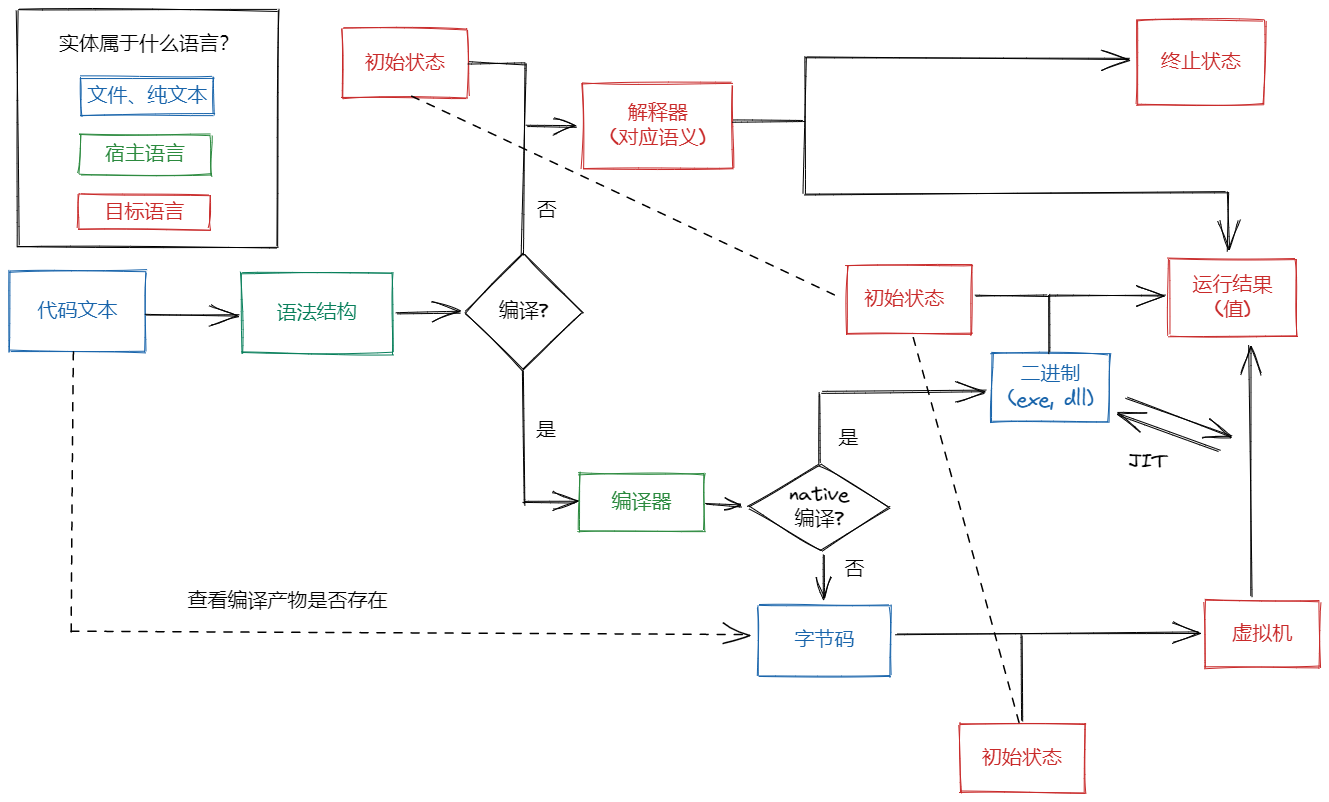
compiler-arch

我们考虑上图的如下流程：

语法结构到字节码。将其用 $X \overset{\text{compile}}{\longrightarrow} I_1 I_2 \cdots I_n$ 的形式描述。
字节码到运行时值，即虚拟机解释。将其用 $S, I \overset{\text{VM}}{\longrightarrow} r, S$ 的形式描述。

我们会先介绍 $\overset{\text{VM}}{\longrightarrow}$ ，但初学者可能因此丢失语境。对此，我们先介绍一个简单例子以方便读者建立直觉。

源码	字节码
`x = add(x, 1)`	`LOAD_VAR add LOAD_VAR x LOAD_CONST 1 LOAD_CONST 2 CALL_FUNCTION 2 STORE_VAR x`