General Programming In Julia Language From An Advanced Standpoint

Julia is a multi-paradigm language which is purely dynamic but supports optional typing.

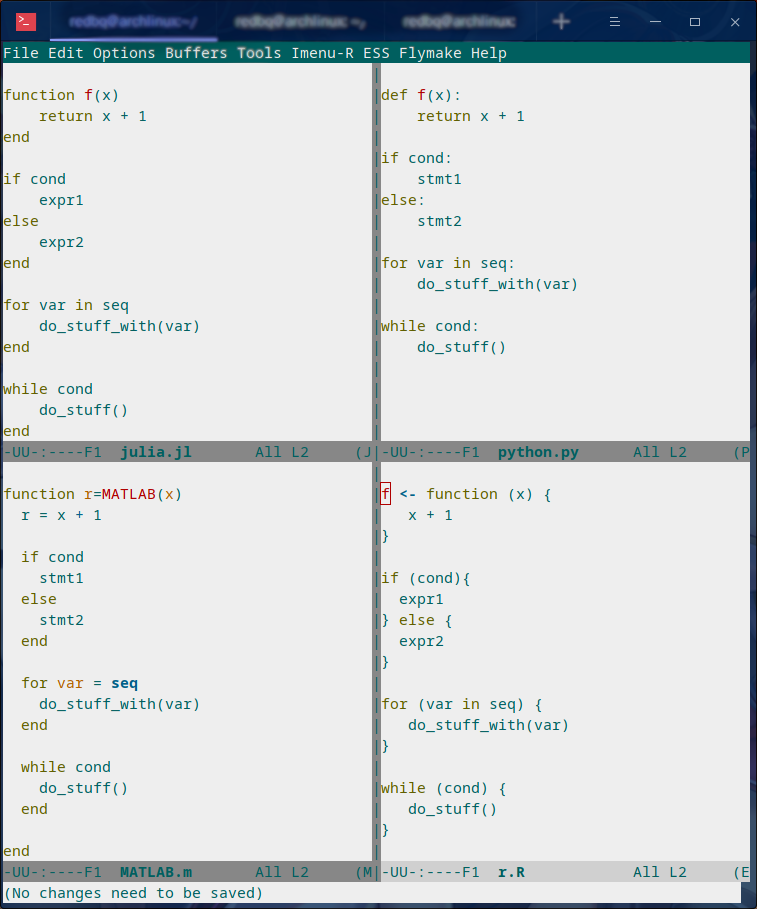
As the introduction of some basic constructs like For-Loop, While-Loop and If-Else and Function akin to those of Python, R or MATLAB, Julia becomes simple and concise, and allows you to work fluently with a fraction of its language features.

../_images/4-langs.png

Although People seldom focus on Julia’s language features other than its high performance(until April 2019), I’d show my point of view of the general programming in Julia.

First-Class

Almost all language constructs in Julia are first-class, upholding more flexible and advanced program composition.

There’re quite a lot of people that has a prejudice against Python for the absense of multi-line lambdas. Although it’s pretty trivial and straightforward to compile multi-line lambdas into normal Python code objects, the frontend, more concretely the mandatory indentation, comfines Python to the expressive power as a result of that statements are rigidly separate from expressions(statements cannot occur in expressions), and then first-class gets missed. There’re other manners to achieve indentation without lossing expression-first like that of ML family and Haskell, but not adopted by Python community yet.

Julia seems to be over-first-class, for all constructs there are expressions and, syntactically there’s no restriction to compose arbitrary constructs. Definitions and computations are distinct from each other in major functional languages, but each of both consists of the other.

 [let y=f(x); (x, y) end for x in points]

 map(
   function map_fn(x)
     # do stuffs
   end,
   points
)


let bind_maybe(a, f) -> a == nothing ? f(a) : nothing,
    (|>) = bind_maybe

    init          |> a ->
    do1_stuffs(a) |> a ->
    ...           |> a ->
    ...           |> a ->
    ...
end

The reason why composability is crucial has been discussed often years on, so I won’t make an another about this topic.

For Julia, first-class also helps when it comes to processing programs as data, which will be unfolded latter in this article.

Polymorphisms of Multiple Dispatch

Julia supports polymorphisms to achieve necessary abstractions and reduce self-repeating, though it does stand apart from those pooular industrial languages.

Multiple dispatch looks like parametric polymorphism, but actually it’s more than the latter.

function usum(x :: Vector{T}) where T
   s = zero(T)
   for each in x
      s += each
   end
   s
end

Overloading is supported as well.

uzero(_ :: Type{Int})     = 0
uzero(  :: Type{Float64}) = 0.0

However, multiple dispatch is more than what I listed above. In fact, type is exclusively a specialized instance of immutable data that could be taken advantage of dispatching, while you can make dispatches via immutable data no matter whether it is a type or others.

struct Const{T}
end

flip(::Type{Const{:even}}) = Const{:odd}
flip(::Type{Const{:odd}})  = Const{:even}

f(::Type{Const{0}}) = Const{:even}
f(::Type{Const{1}}) = Const{:odd}
f(::Type{Const{N}}) where N = f(Const{N-1}) |> flip

With above codes, we can statically compute parity of numbers, just as expected.

julia> @code_warntype f(Const{2})

Body::Type{Const{:even}}
  1 ─     return Const{:even}

Note that when multiple dispatch fails at static inferences, it’ll behave as dynamic dispatch like Python’s.

A Big Step Forward in AST Manipulations

Julia does a lot on ASTs, e.g., analysis, substitution, rewriting, and so on.

As we’ve introduced the laws of AST interpolations, you might know that we can generate ASTs like following codes instead of in purely constructive manner.

ex0 = [1, 2, 3]
ex1 = :[1, 2, 3]

ex2 = :($ex0 + 1)
# :([1, 2, 3] + 1), [1, 2, 3] here is already evaluated before interpolation.

ex3 = :($ex1 + 1)
# :([1, 2, 3] + 1)

That’s not that cool for there’re also other approximate supports in other languages in current stage.

The advance is at the deconstructing of ASTs, which extremely impacts the way we could analyse ASTs.

Think about a case that you’d like to collect positional arguments and keyword arguments from some function callsites.

get_arg_info(:(f(a, b, c = 1; b = 2))) # => ([:a, :b, :(c = 1)], [:(b = 2)])
get_arg_info(:(f(args...; kwargs...))) # => ([:(args...)], [:(kwargs...)])
get_arg_info(:(f(a, b, c)))            # => ([:a, :b, :c], [])

How will you achieve this task?

Attention! No matter how you’ll deal with it, think about whether you need to get a prerequisite about Julia AST structures? Say, you have to know Expr (a.k.a one of the most important Julia AST types) has 2 fields, head and args, or you have to understand the structure of a.b is

Expr
head: Symbol .
args: Array{Any}((2,))
  1: Symbol a
  2: QuoteNode
    value: Symbol b

instead of

Expr
head: Symbol .
args: Array{Any}((2,))
  1: Symbol a
  2: Symbol b

, or you have to make it clear that in vector literals, there’re

Vector/Matrix Literals
Julia code AST structure
[1 2 3] 
Expr
head: Symbol hcat
args: Array{Any}((3,))
  1: Int64 1
  2: Int64 2
  3: Int64 3
[1, 2, 3] 
Expr
head: Symbol vect
args: Array{Any}((3,))
  1: Int64 1
  2: Int64 2
  3: Int64 3
[1; 2; 3] 
Expr
head: Symbol vcat
args: Array{Any}((3,))
  1: Int64 1
  2: Int64 2
  3: Int64 3

[1 2; 3 4] or [1 2
               3 4]

Expr
  head: Symbol vcat
  args: Array{Any}((2,))
    1: Expr
      head: Symbol row
      args: Array{Any}((2,))
        1: Int64 1
        2: Int64 2
    2: Expr
      head: Symbol row
      args: Array{Any}((2,))
        1: Int64 3
        2: Int64 4

To be honest, there’re so many detailed rules about the strcutrue, but is it really necessary to know them all if you’re planning to work with Julia ASTs(including analysis about their strcutrues)?

No! Absolutely no! Although I know many of you older Julia guys are always checking and decomposing ASTs with your vast knowledge about Julia internals , I’d suggest you sincerely to start using MLStyle.jl, for the sake of your efficiency.

At here, I’d introduce MLStyle’s AST Manipulations to you via giving some impressive examples. For sure this package will be displaced by some better alternative one day, but the underlying methodology wouldn’t change at all. Don’t open the link immediately now, just follow my introduction now, you don’t need to care much about a specific package or framework, but its core idea.

A tremendous inspiration occurred to me on one day in the last year(2018) that, what if we can deconstruct ASTs just as how they’re constructed.

In fact, You don’t have to know accurately about all AST structures when you start using corresonding syntaxes, like you just write

a = [1, 2, 3]
b = [1 2 3]
c = [1; 2; 3]
d = [1 2; 3 4]

Does you have to know what will the their AST look like? No.

A classmate of mine who knows only mathematics and has never got an experience in programming before can still write such codes fluently to complish his linear algebra homeworks, but he does feel annoyed when I try to explain the concepts of ASTs and how the ASTs he just written would look like.

You might have notice the importance of using syntactic components, yes, it’ll simply makes progress in the history we manipulate programs as data.

Pattern matching is an essential infrastructure in modern functional languages, which reduces the complexity of almost all logics via deconstructing data as how data is constructed.

Okay, this sentence occurred twice now:

deconstructing data as how data is constructed.

Remember it, and it’s our principle in this section.

Let’s think about how ASTs are constructed?

Firstly, we can write raw ASTs, write them literally.

ex = :(a + 1)
ex = :[1 2 3]

Next, there are syntactic AST interpolations.

ex = :[1, 2, 3]
ex = :($ex + 1) # :([1, 2, 3] + 1)

That’s enough. Now, let’s introduce a @match. This syntax may be deprecated in the better alternative in your time, but you must be able to simply make an equivalence or superior via the better one with the new start-of-the-art pattern matching package at the time you’re reading this article.

@match value begin
  pattern1 => value1
  pattern2 => value2
end

To support match literal ASTs, we must get a true with following codes,

# rmlines is a function that removes all line number nodes in an AST.
# you can fetch it here : https://github.com/thautwarm/MLStyle.jl#preview

@match rmlines(:(let x = 1; x end)) begin
  :(let x = 1; x end) => true
  _ => false
end

Think about the principle we’ve figured out, okay, I’d stress it again here as I’m a shabby repeater:

deconstructing data as how data is constructed.

Then

v = :[1, 2, 3]
ex = :($v + 1)
@match ex begin
  :($v + 1) => v == :[1, 2, 3]
  _ => false
end

Oooh! Do you understand it? Does it make sense in your opinion?

AST interpolation corresponds to constructing, while AST interpolations occur in pattern it’s regarded as deconstructing. We can call it “AST extractions”.

Now, let’s turn back to the original question, to implement get_arg_info mentioned previously.

We should at first introduce some examples about constructing in the case of get_arg_info.

If we want to pass arguments to f(a, b; c, d), we can use

f(a, b; c, d) = a + b + c + d
args = [1, 2]
kwargs = Dict(:c => 1, :d => 2)
f(args... ; kwargs...)

, which produces a result 6.

Notice about the form f(args...; kwargs...), it might indicates that in AST level, positional arguments and keyword arguments are stored in arrays, respectively.

Let’s have a try:

args = [:a, :b]
:(f($(args...)))

And you’ll get an output exactly as

:(f(a, b))

Good job, now we use MLStyle’s @match, following the rule deconstructing data as how data is constructed as well.

args = [:a, :b]
@match :(f($(args...))) begin
   :(f($(args...))) => args == [:a, :b]
   _ => false
end

Then you get a true as output.

Think a while, and check the final implementation of get_arg_info:

get_arg_info(ex) = @match ex begin
     :($name($(args...); $(kwargs...))) ||
     :($name($(args...))) && Do(kwargs = []) => (args, kwargs)

     _ => throw("invalid input")
end

|| denotes the so-called Or-Pattern.

Limitation: Absence of Function Types

Julia is an ideal language for quite many domains but, not for all.

For people who’re used to functional programming languages, especially for the groups that tilts the advanced type-based polymorphisms(type classes’ instance resolution, implicit type variables, higher-kinded-polymorphisms, etc.), there’s an essential necessity of the dedicated function type.

On and off, I’ve attempted a lot with my friends to emulate those advanced type-based polymorphisms in Julia, but finally we noticed that without implicit inferences on functions, only dynamic typing and multiple dispatch are far from being sufficient.

In Julia, each function has its own type which is a subtype of Function, which prevents making abstractions for functions from common behaviours in type level. The worse is, these abstractions on functions in type level have been proven pervasive and fairly useful by academic world for about 10000 year, and perform a role like arithmetic operation in our educations.

In Haskell, the type signature of a function does help in semantics side. Following Haskell code allows users to automatically generate tests for a given type/domain by taking advantage of properties/traits of the type/domain.

import Control.Arrow
import Data.Kind

newtype MkTest (c :: * -> Constraint) a = MkTest {runTest :: a}

class TestCase (c :: * -> Constraint) a where
    samples      :: c a => MkTest c [a]
    testWith     :: c a => (a -> Bool) -> MkTest c [(a, Bool)]
    testWith logic =
        MkTest $ map (id &&& logic) seq
        where
            seq :: [a]
            seq = runTest (samples :: MkTest c [a])

type TestOn c a = c a => (a -> Bool) -> MkTest c [(a, Bool)]

Now I’m to illustrate how Haskell achieves a perfectly extensible and reasonable automatic test generator, through following instances(terminology in Haskell, other than a synonym of “example”), using function types to achieve polymorphisms that absolutely Julia cannot make so far(Juliav1.1).

instance TestCase Enum a where
    samples = MkTest . enumFrom . toEnum $ 0

instance TestCase Bounded a where
    samples = MkTest [maxBound, minBound]

We has now made instances for TestCase on the constraints(a.k.a Type Classes) Enum and Bounded.

For the readers who’re not that familiar to Haskell, you could take constraints in Haskell as traits(in Rust) or loose-coupled interfaces.

Once a type is under constraint Enum, you can enumerate its values, plus Bounded is a constraint capable of making sure that the maximum and minimum are available(via maxBound and minBound). instance TestCase Enum a denotes for all concrete type a, make the constraint TestCase on constraint Enum and type a. Yes, TestCase is also a constraint, a constraint among other constraints and types.

So far our test generator has been already finished, a bit too fast, right? That’s how Haskell matters: pragmatic, productive.

We can then make tests with above codes, taking advantage of properties/traits of our data types:

onEnumerable :: TestOn Enum a
onEnumerable logic = testWith logic

intTest :: Int -> Int
intTest x = x ^ 2 + 4 * x + 4 == (x - 2)^2

boolTest :: Bool -> Bool
boolTest x = True

main = do
  putStrLn . show . take 10 . runTest $ onEnumerable intTest
  putStrLn . show . runTest $ onEnumerable boolTest
  return ()

which outputs

[(0,True),(1,True),(2,True),(3,True),(4,True),(5,True),(6,True),(7,True),(8,True),(9,True)]
[(False, True), (True, True)]

Take care that the I did nothing to generate test sets, but passing off the function intTest and boolTest to specify the test logics. I solely said that I want to test data types on their enumerable traits(onEnumerable), then the polymorphic automatic test generator took advantage of functions’ type signatures(intTest: Int -> Bool, boolTest: Bool -> Bool), and all tasks finished.

Turn back to Julia side, although Haskell does a lot implcits, multiple dispatch can often emulate them successfully(without strongly typed and static checking though). The problem is at the absense of function types, as we cannot take advantage of their type information to engage dispatching.

Some tentative but incomplete workaround could be made through following idea:

import Base: convert
struct Fn{Arg, Ret, JlFuncType}
    f :: JlFuncType
end

@inline Fn{Arg, Ret}(f :: JlFuncType) where {Arg, Ret, JlFuncType} = Fn{Arg, Ret, JlFuncType}(f)

@generated function (f :: Fn{Arg, Ret, JlFuncType})(a :: Arg) :: Ret where {Arg, Ret, JlFuncType}
  quote
      $(Expr(:meta, :inline))
      f.f(a)
  end
end

convert(Fn{Arg, Ret, JlFuncType}, f :: JlFuncType) where {Arg, Ret, JlFuncType} = Fn{Arg, Ret, JlFuncType}(f)

This is a considerably efficient function type implementation according to FunctionWrappers.jl, However, the problem is that its usage is quite unfriendly for peope have to manually annotate disturbingly much.

To address the polymorphism problems, the major methods(type-based) from current academic world won’t work in Julia, and you should pave the way for a LISP-flavored “polymorphism”, in other words, use macros frequently.