高观点下的Julia泛用编程
高观点下的Julia范用编程
Julia是一个支持可选类型标注的纯动态多范式语言。
由于其引入的一些像For循环,While循环, If循环, 函数等的基本语言构造, 与Python, R或是MATLAB类似, Julia变得简单和简洁, 使得你可以仅用它一部分的语言特性便流畅地工作。
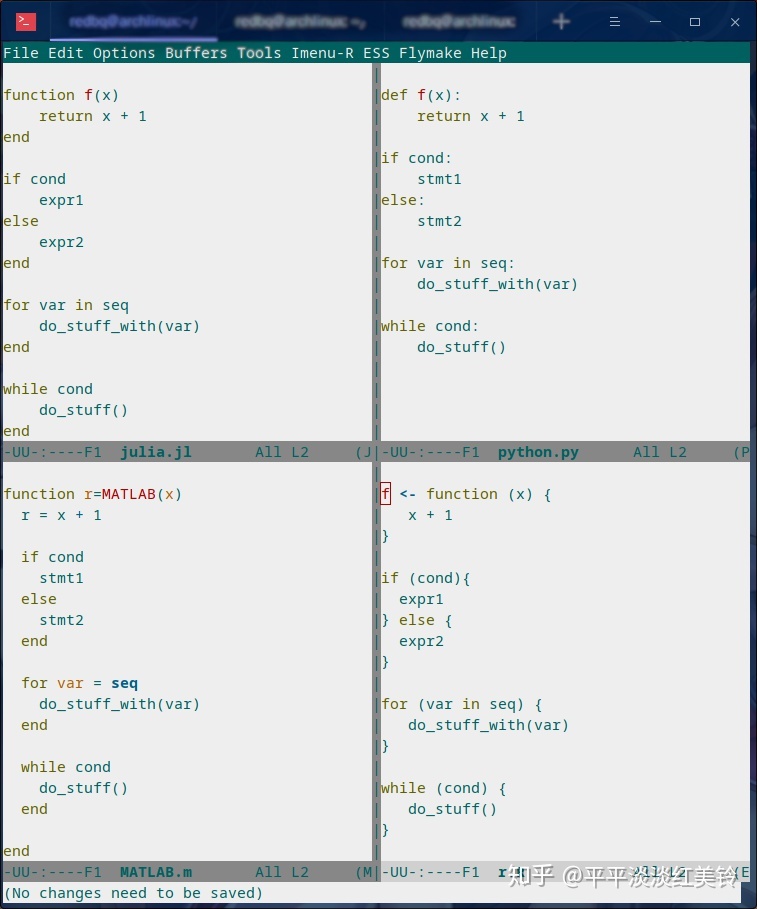
尽管人们很少关注Julia除开高性能以外的语言特性(截止2019年4月),我的角度却是在它的泛用编程方面。
First-Class
Julia中, 几乎所有的语言构造都是first-class的,使得语言的灵活性和可组合性得以彰显。
很多人对于Python缺少多行lambda这事抱有偏见。尽管把多行lambda编译到通常的Python code object是相当平凡和直接的, 前端,更具体点,强制缩进,通过严格分离表达式和语句(语句无法出现在表达式中), 限制了Python的表达力, 也失去了 first-class。其他的没有限制expression-first的语言缩进方式是有的,例如ML家族和Haskell, 但还没有被Python社区所采纳。
Julia看起来有点过于first-class, 因为它所有的构造都是表达式, 在语法上讲并不限制任意语言构造的组合。定义和计算在很多主流的函数式语言中是分离的,只是两者的组成里各自包含对方。
[let y=f(x); (x, y) end for x in points]
map(
function map_fn(x)
# 做一些事情
end,
points
)
let bind_maybe(a, f) -> a == nothing ? f(a) : nothing,
(|>) = bind_maybe
init |> a ->
do1_stuffs(a) |> a ->
... |> a ->
... |> a ->
...
end为什么可组合性很关键的原因多年来被经常讨论,所以我不会就此再整一个。 对于Julia而言,first-class在涉及代码即数据时会很有用, 文章稍后展开这点。
多重分派的多态
Julia支持多态,以实现必要的抽象,减少self-repeating,尽管和那些流行的工业语言有着明显的不同。
多重分派看起来有点像参数化多态, 但实际上其含义比起后者要多。
function usum(x :: Vector{T}) where T
s = zero(T)
for each in x
s += each
end
s
end重载也是可以的。
uzero(_ :: Type{Int}) = 0
uzero( :: Type{Float64}) = 0.0然而多重分派不仅仅是我上面列举的。实际上类型只是可分派的不可变数据的一种特殊实例, 你能够用不可变的数据来分派,不管它是类型还是别的什么劳什子。
struct Const{T}
end
flip(::Type{Const{:even}}) = Const{:odd}
flip(::Type{Const{:odd}}) = Const{:even}
f(::Type{Const{0}}) = Const{:even}
f(::Type{Const{1}}) = Const{:odd}
f(::Type{Const{N}}) where N = f(Const{N-1}) |> flip使用上述代码,我们可以如期地静态计算数字的奇偶性。
julia> @code_warntype f(Const{2})
Body::Type{Const{:even}}
1 ─ return Const{:even}注意,如果多重分派在静态推断上失败,它将表现得如同Python中的动态分派一般。
Full-Featured的宏
宏是实现代码复用的极少途径之一, 也是为什么有一些程序员千百倍高效于其他人的原因。
julia> macro gen_var(n :: Int, f)
defs = [Expr(:(=), Symbol("var", i), :($f($i))) for i in 1:n]
esc(Expr(:block, defs..., nothing))
end
@gen_var (macro with 1 method)
julia> f(x) = x * 10 - 2
f (generic function with 1 method)
julia> @gen_var f (x * 10 - 2)
julia> var1
8
julia> var2
18宏,从AST到AST的函数
一旦你知道宏是从AST到AST的函数后,Julia的宏便不再神秘。
macro f(x)
println(x)
:($x + 1)
end
@assert (@f 1) == 2上述代码展示了Julia宏的一个生动例子。首先 macro 关键字引导宏变换规则的定义,而@f标记来对应宏规则的调用点。
你可能会问为什么(@f 1 == 2, 因为宏@f的返回值是一个AST,看起来让它和整数2相等有点魔幻。
认真看@assert (@f 1) == 2。由于宏调用是从内到外依次处理的,我们首先处理的应该是@f 1。
(function f(x)
println(x)
:($x + 1) => :(1 + 1)
end)(1)上面这步,在执行AST到AST的函数f, 即宏@f, 的时候,还会写stdio.
随后,由于我们已经拿到一个输出, AST :(1 + 1), 设想我们用它置换先前代码中的@f 1,这会产生一个@assert $(:(1 + 1)) == 2, 化简它,然后我们得到@assert (1 + 1) == 2。
你可能会问为什么@assert :(1 + 1) == 2, 好问题,我们深入研究一个。
想想如果你从宏调用处返回的是一个运行时AST,它不会被转换为要编译的代码,以至于这样的宏会变得完全没有用。
如果我们unquote宏的返回,
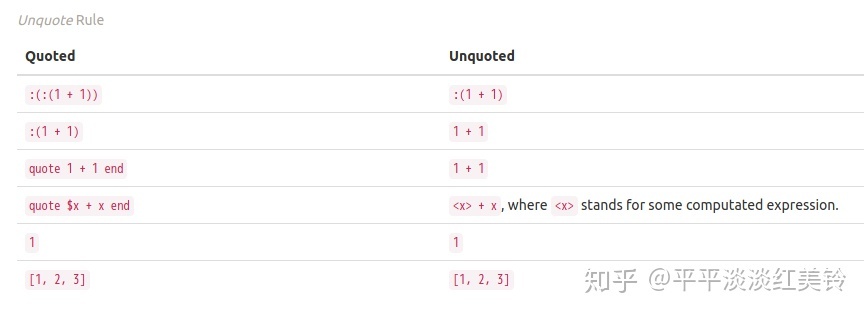
上面的表格揭示了AST插值的规则,以及,很明显这里有点东西: 如果我们说一个表达式被quote了N次,那么它的插值,作为一个表达式被quote了max(0, N - 1)次。
作用域和卫生
只要你站在宏是AST到AST的函数这个观点下, 宏(返回的AST)的作用域规则会很简单。
julia> module A
var = 0
macro ma()
quote
var
end
end
end
julia> var = 5555
julia> A.@ma
0
julia> using .A: @ma
julia> @ma
0我这儿要说的第一点是, 宏返回的表达式是在宏定义处的模块被求值的。
macro assign_y(x)
:(y = $x)
end
function f(x)
@assign_y x
y
end
f(1)你可能期望这代码能预期跑通,但很不幸,不行,只会给你扔一个
ERROR: UndefVarError: x not defined
Stacktrace:
[1] f(::Int64) at ./REPL[6]:2
[2] top-level scope at none:0这里的原因是,AST插值会被预先处理,以确保所有的裸符号(没有包在QuoteNode和更深的quote中)会被 转换到像##a#168这样有点奇怪的mangled符号(也被称为gensym). 同时,Julia干这事儿的原因, 是为了默认避免为局部作用域产生新的可见符号。
想想你想打算在计算了值后进行打印的宏:
macro with_logging(expr)
quote
a = $expr
@info :logging a
a
end
end我们没把符号a转换到类似##a#167这样子,假如你已经在你的代码里定义了a呢?
function x5(a) # 把它当作乘5
x2 = @with_logging 2a
x3 = @with_logging 3a
x2 + x3
end
my_func(1)你可以看见如果宏with_logging不转换宏定义体里写的a, 你将会得到x5(1) == 8而不是x5(1) == 5。
就是这样,我们叫这样的宏,卫生宏。
但是还有一些上下文有关的代码生成,你想要在多个代码生成函数中共享作用域。一个有点东西的例子是 我的MLStyle, 它实现了我自学习编程以来的一个梦想,即能够使用一个高性能且可扩展(可自定义)的模式匹配。 在这个包里,在编译模式的时候,我会使用手动的gensym而不是依靠卫生宏,因为我可能在不同的会生成代码的函数里 访问某些指定的符号。
在这种情况下,人们想要产生可以污染作用域的符号,Julia提供来一种转义(escaped)机制来避免gensym.
macro assign_y(x)
esc(:(y = $x))
end
function f(x)
@assign_y x
y
end
f(1) # 1先前的代码, 在返回的AST上补充了一个esc的调用后,便可以正常工作。
其他对Julia宏有用的知识点
@__MODULE__会给当前模块。- 当你想要控制求值(evaluate) AST的模块时,你可以用
moduleX.eval(expr)或者@eval moduleX expr。 - 尽管我们已经知道宏是函数,一些需要强调的事情是,这里有两个隐式的参数:
__module__和__source__,__module__是你调用该宏时所处的模块,__source__是该宏调用的行号结点。
AST操作上的进步
Julia在AST上搞得很多,比如,分析,替换,重写,诸如此类。
由于我们已经介绍来AST的插值规则,你可能已经知道我们能像下面代码那样产生AST,而不是用纯粹的构造性的方式。
ex0 = [1, 2, 3]
ex1 = :[1, 2, 3]
ex2 = :($ex0 + 1)
# :([1, 2, 3] + 1), [1, 2, 3] here is already evaluated before interpolation.
ex3 = :($ex1 + 1)
# :([1, 2, 3] + 1)这不是那么酷炫,因为现阶段其他的语言也有接近这样的支持。
进步在于对于AST的解构, 这极大地影响了我们可以用来分析AST的方式。
考虑这样一种情况,你想要从函数调用处搜集所有的位置参数和关键字参数。
get_arg_info(:(f(a, b, c = 1; b = 2))) # => ([:a, :b, :(c = 1)], [:(b = 2)])
get_arg_info(:(f(args...; kwargs...))) # => ([:(args...)], [:(kwargs...)])
get_arg_info(:(f(a, b, c))) # => ([:a, :b, :c], [])你会如何干这事?
注意!无论你打算如何处理它,想想你是否需要对Julia的AST有一个预先的了解? 比方说,你不得不知道 Expr(正是Julia AST的类型中最为重要的一种)有两个fields, head和args, 或者你不得不理解 a.b的结构是
Expr
head: Symbol .
args: Array{Any}((2,))
1: Symbol a
2: QuoteNode
value: Symbol b而非
Expr
head: Symbol .
args: Array{Any}((2,))
1: Symbol a
2: Symbol b或者你不得不搞清楚,对于向量的字面量,有
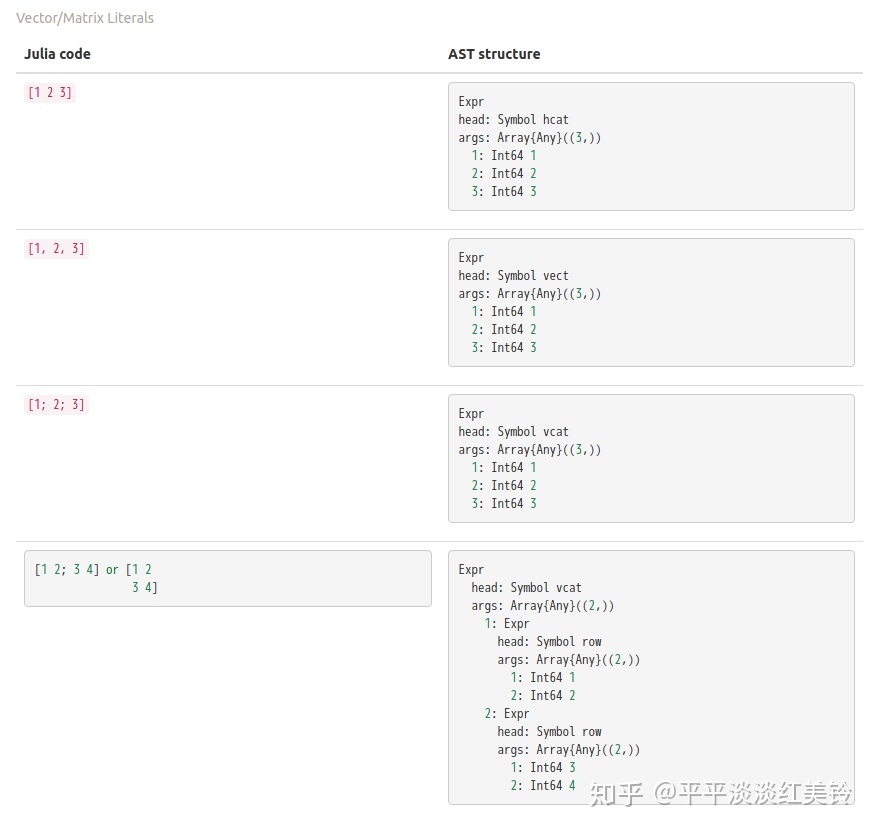
说实在的,这里有这么多的关于结构的细节问题,但是当你需要使用 Julia AST工作(包括对结构的分析)时,你真的有必要知晓所有东西吗?
不!当然是不用的!尽管我知道, 你们中一些时间更长的Julia使用者, 总是通过你们 丰富的Julia internal知识来检查以及分解AST,但我真诚地建议你开始使用MLStyle.jl, 为了你的效率起见。
在此,我会介绍MLStyle的AST操作 来给你一些有印象深刻的例子。 当然,这个包会在某一天被更好的替代,但其本质的方法论不会偏离分毫。现在不要马上打开链接,跟着我的介绍走,你不需要 对一个具体的包或者框架过分在意,除了它的核心思想。
一个重要的灵感在2018年的某一天降临了我: 假如我们可以用构造AST的方式去解构AST,会怎么样?
实际上,你并不需要精确地知道所有AST的结构,在你开始写它对应的语法的时候。比如你可以写
a = [1, 2, 3]
b = [1 2 3]
c = [1; 2; 3]
d = [1 2; 3 4]你需要知道他们的AST长什么样吗?不用的。
我有个仅仅学数学,此前从来不接触编程的同学, 也可以流畅地写出这样的代码来解决他的线性代数作业, 但当我尝试跟他讲AST的概念, 以及他刚写的代码的AST长什么样时,他感觉非常恼火。
你或许已经注意到了使用语法要素的重要性。是的,在像数据一样处理代码的方面,它将 取得巨大的进步。
模式匹配是现代函数式语言中的一个基本设施, 通过像构造数据一样进行解构, 它能够降低处理几乎所有逻辑时的复杂性。
好的,这句话出现两次了:
像构造数据一样进行解构.
记住它,它是我们这一节的根本准则。
让我们想想AST是怎么被构造的?
首先,我们可以写生(类似生开水的生)的AST,字面地写它。
ex = :(a + 1)
ex = :[1 2 3]然后,我们有AST插值。
ex = :[1, 2, 3]
ex = :($ex + 1) # :([1, 2, 3] + 1)这就够了。现在让我们介绍@match. 这个语法可能会在你的时间点下被更好的类似物替代, 但利用你读这篇文章时最好的模式匹配库, 你必然可以轻易地实现等价乃至更好的东西。
@match value begin
pattern1 => value1
pattern2 => value2
end为了支持匹配字面量AST, 我们必须要求下列代码返回true.
# rmlines is a function that removes all line number nodes in an AST.
# you can fetch it here : https://github.com/thautwarm/MLStyle.jl#preview
@match rmlines(:(let x = 1; x end)) begin
:(let x = 1; x end) => true
_ => false
end想想我们已经建立其的那个根本准则, 好吧,我又会重复它一遍因为我是个 劣质的复读机:
像构造数据一样进行解构.
然后
v = :[1, 2, 3]
ex = :($v + 1)
@match ex begin
:($v + 1) => v == :[1, 2, 3]
_ => false
end嗷! 你懂吗? 你感觉这个有点东西吗?
AST插值对应着构造,那么出现在模式中的AST插值就表示解构。我们可以把它叫做"AST摘要"。
现在,然后我们回到最开始的问题,实现之前提到的get_arg_info。
首先, 我们用一些例子来介绍get_arg_info情形下的构造。
f(a, b; c, d) = a + b + c + d
args = [1, 2]
kwargs = Dict(:c => 1, :d => 2)
f(args... ; kwargs...)这会给出结果六。
注意形式f(args...; kwargs...), 这貌似表示,在AST层面上,位置参数和关键字参数都是用数组来存的。
试试:
args = [:a, :b]
:(f($(args...)))然后你能够拿到一个输出,恰好是
:(f(a, b))很好,好极了。现在我们再用MLStyle的@match, 还是遵守像构造数据一样进行解构的规矩。
args = [:a, :b]
@match :(f($(args...))) begin
:(f($(args...))) => args == [:a, :b]
_ => false
end然后你拿到一个true的输出。
要多想。然后看看get_arg_info的最终实现:
get_arg_info(ex) = @match ex begin
:($name($(args...); $(kwargs...))) ||
:($name($(args...))) && Do(kwargs = []) => (args, kwargs)
_ => throw("invalid input")
end|| 表示所谓的Or模式(or-pattern)。
缺憾: 函数类型的缺失
Julia对很多领域来说是一门理想的语言,但,不是所有。
对那些习惯函数式语言的人,尤其对那种倾向于使用基于类型的高级多态(type class的实现resolve, 隐式类型变量, 高阶类型抽象等), 专门的函数类型是一种基本到不能再基本的东西。
断断续续地,我和朋友做了很多尝试,来模拟那些高级的类型多态。但最终我们发现没有隐式推导,仅仅是 动态类型和多重分派还差得很远。
在Julia里,每一个函数都有它自己的类型,并且是Function的子类型,阻止来我们在类型层面去抽象函数们的公共 行为。更糟糕的是,这些类型层面对函数的抽象,已经被学界在一万年前证明是无处不在且极为有用的了,还扮演着 一个像是我们学习过程中四则运算一般的角色。
在Haskell中,函数的signature会对语义起作用。
下面的Haskell代码允许用户对给定的类型,通过这些类型上的性质/特质,来自动生成测试。
import Control.Arrow
import Data.Kind
newtype MkTest (c :: * -> Constraint) a = MkTest {runTest :: a}
class TestCase (c :: * -> Constraint) a where
samples :: c a => MkTest c [a]
testWith :: c a => (a -> Bool) -> MkTest c [(a, Bool)]
testWith logic =
MkTest $ map (id &&& logic) seq
where
seq :: [a]
seq = runTest (samples :: MkTest c [a])
type TestOn c a = c a => (a -> Bool) -> MkTest c [(a, Bool)]现在我会用Haskell代码来实现一个完美的可扩展的自动测试生成器, 通过下面的实例(Haskell中的术语), 利用函数类型,来实现当前Julia(v1.1)中无法实现的多态。
instance TestCase Enum a where
samples = MkTest . enumFrom . toEnum $ 0
instance TestCase Bounded a where
samples = MkTest [maxBound, minBound]现在我们为TestCase在约束(即Type Class)Enum和Bounded上创建实例。
对于不熟悉Haskell的读者来说,你可以把Haskell中的约束理解为(Rust中的)trait或者松耦合的interface。
一旦类型处于Enum的约束下,你就可以枚举它的取值, 以及Bounded是一种能够确保类型中最大和最小可以访问的约束(通过 maxBound和minBound)。instance TestCase Enum a表示对于所有的具体类型(非约束)a,为约束TestCase在约束Enum 和类型a上建立约束。是的, TestCase也是一种约束, 一个在其他约束和类型上建立约束的约束。
目前为止,我们的测试生成器已经搞定来,有点突然,对吧? 这就是Haskell: 务实, 生产力高效。
我们可以用上面的代码搞一些测试,利用我们数据类型的性质/特质。
onEnumerable :: TestOn Enum a
onEnumerable logic = testWith logic
intTest :: Int -> Int
intTest x = x ^ 2 + 4 * x + 4 == (x - 2)^2
boolTest :: Bool -> Bool
boolTest x = True
main = do
putStrLn . show . take 10 . runTest $ onEnumerable intTest
putStrLn . show . runTest $ onEnumerable boolTest
return ()这会输出
[(0,True),(1,True),(2,True),(3,True),(4,True),(5,True),(6,True),(7,True),(8,True),(9,True)]
[(False, True), (True, True)]注意我在生成测试集上啥也没做,除了把说明测试逻辑的intTest和boolTest传过去。我只是 说了我想要测试他们的可枚举特质(onEnumerable), 然后多态的自动测试生成器利用函数signature (intTest: Int -> Bool, boolTest: Bool -> Bool), 然后一切搞定。
回到Julia侧,尽管Haskell做了很多隐式操作,多重分派总是可以成功地模拟它(但没有强类型和静态检查)。 问题在于函数类型的缺失,因为我们不能够利用它的类型信息参与分派。
下面的思路提供了一些暂时且不完整的解决方案:
import Base: convert
struct Fn{Arg, Ret, JlFuncType}
f :: JlFuncType
end
@inline Fn{Arg, Ret}(f :: JlFuncType) where {Arg, Ret, JlFuncType} = Fn{Arg, Ret, JlFuncType}(f)
@generated function (f :: Fn{Arg, Ret, JlFuncType})(a :: Arg) :: Ret where {Arg, Ret, JlFuncType}
quote
$(Expr(:meta, :inline))
f.f(a)
end
end
convert(Fn{Arg, Ret, JlFuncType}, f :: JlFuncType) where {Arg, Ret, JlFuncType} = Fn{Arg, Ret, JlFuncType}(f)根据FunctionWrappers.jl, 这是一个相当高效的函数类型实现。
然而,问题在于它的使用非常不友好,需要人们进行大量的手工类型标注,这很烦人。
对于多态问题的解决尝试, 学术界的主流方案(基于类型的)在Julia这里不能奏效。你得准备收拾收拾 去搞LISP风格的"多态", 我是说你得经常写宏。
